Bayesian Optimization
Automatic explore-exploit tradeoff
Bayesian Optimization
Goal: minimize unknown function $\phi$ in as few evaluations as possible
- Build posterior $f \given y$ using data $(x_1,\phi(x_1)),..,(x_n,\phi(x_n))$
- Choose $$ \htmlClass{fragment}{ x_{n+1} = \argmax_{x\in\c{X}} \alpha_{f\given y}(x) } $$ using the acquisition function $\alpha_{f\given y}$, built from the posterior
Principle of Separation: prediction and decision
Gaussian Processes
Probabilistic formulation provides uncertainty
Extrapolation and Uncertainty
Neural network baseline
Extrapolation and Uncertainty
Gaussian process: squared exponential kernel
Extrapolation and Uncertainty
Gaussian process: polynomial kernel
Extrapolation and Uncertainty
Neural network ensemble
Extrapolation and Uncertainty
Gaussian process: stationary kernel
Gaussian process: polynomial kernel
Ensemble
Models allow us to engineer different uncertainty behavior
For more on this, check out my UAI tutorial
How can we engineer different decision-making behavior?
Thompson Sampling
Same model, different decisions, similar performance
What about other settings?
Example Setting: Function Networks for Molecule Design
Use Bayesian optimization to find good candidates in generative model's latent space
Challenge: multi-stage evaluation with partial feedback
Challenges
Modeling:
- Uncertainty and generalization
- Symmetries and geometry
- Smoothness and non-uniformity
- Causal information
Decision-making:
- Multi-stage feedback
- Scheduling and asynchronicity
- What kind of uncertainty is needed?
- Adversarial objectives
- Theoretical guarantees and empirical performance
If we succeed...
If we succeed...
Explore-exploit tradeoffs: a key difficulty in reinforcement learning
If we succeed...

Today's most impressive systems: a combination of learning and search
Search and decision: less appreciated side of Rich Sutton's Bitter Lesson
AlphaGo and AlphaProof: discrete - tree search
If we succeed...
Machine learning: predicted antibiotic activity in halicin, prev. studied for diabetes
Shown in mice to have broad-spectrum antibiotic activity
Figure and results: Stokes et al. (Cell, 2020)
Challenges: Angles of Attack





To understand decision, we should pursue every viable angle of attack
The Pandora's Box Gittins Index:
a new acquisition function design principle
Joint work with Qian Xie, Raul Astudillo, Peter Frazier, and Ziv Scully
Cost-aware Bayesian Optimization
Goal: minimize unknown function $\phi$ in as few evaluations as possible
- $\phi$: drawn randomly from the prior
- $c(x_t)$: cost of getting new data point, expected budget constraint
Algorithm:
- Build posterior $f \given y$ using data $(x_1,\phi(x_1)),..,(x_t,\phi(x_t))$
- Find optimum of acquisition function $\alpha_{f\given y}$ and evaluate $\phi$ at $$ \htmlClass{fragment}{ x_{t+1} = \argmax_{x\in\c{X}} \alpha_{f\given y}(x) } $$
Optimal choice $x_{t+1}$ and when to stop: intractable dynamic program
Expected improvement per unit cost
Cost-aware baseline: expected improvement per unit cost $$ \begin{aligned} \htmlClass{fragment}{ \alpha_{t}^{\f{EIPC}}(x) } & \htmlClass{fragment}{ = \frac{\f{EI}_{f\given y_1,..,y_t}(x; \max_{1\leq\tau\leq t} y_\tau)}{c(x)} } & \htmlClass{fragment}{ \f{EI}_\psi(x; y) } & \htmlClass{fragment}{ = \E \max(0, \psi(x) - y) } \end{aligned} $$
Invariant to multiplying costs by a scalar: do we want this behavior?
Cost-aware analog of expected improvement:
- Expected improvement: derived in non-cost-aware setting via one-step approximation to intractable dynamic program
What if I told you this dynamic program can sometimes be solved exactly?
Cost-aware Bayesian Optimization: a simplified setting
Assumptions:
- Cost-per-sample problem: algorithm decides when to stop
- Reward once stopped: best observed point (simple regret)
- Distribution over objective functions is known
- $X$ is discrete, $f(x_i)$ and $f(x_j)$ for $x_i \neq x_j$ are independent
These are restrictive! But they lead to an interesting, general solution
This setting: Pandora's Box problem from economics
Whether to open Pandora's Box?
Solving Pandora's Box
Consider: one closed vs. one open box
Should we open the closed box? Maybe!
Depends on costs $c$, reward distribution $f$, and value of open box $g$
Consider: one closed vs. one open box
One closed vs. open box: Markov decision process
Optimal policy: open if $\f{EI}_f(x; g) \gt c(x)$
Consider: one closed vs. one open box
Consider how optimal policy changes as a function of $g$
If both opening and not opening is optimal: $g$ is a fair price
Define: $\alpha^\star_t(x) = g$ where $g$ solves $\f{EI}_f(x; g) = c(x)$
Solution: Gittins Index
Theorem (Weitzman, 1979). Let:
- $X$ be a finite set,
- $f : X \to \R$ be a finite-mean random function for which $f(x)$ is independent of $f(x')$ for $x \neq x'$,
- $c : X \to \R_+$, without loss of generality, be deterministic.
Then, for the cost-per-sample problem, the policy defined by maximizing the Gittins index acquisition function $\alpha^\star$ with its associated stopping rule is Bayesian-optimal.
Expected Budget-constrained vs. Cost-per-sample
Gittins index $\alpha^\star$: optimal for cost-per-sample problem
- What about expected budget-constrained problem?
Theorem. Assume the expected budget constraint is feasible and active. Then there exists a $\lambda \gt 0$ and a tie-breaking rule such that the policy defined by maximizing the Gittins index acquisition function $\alpha^\star(\.)$, defined using costs $\lambda c(x)$, is Bayesian-optimal.
Proof idea: Lagrangian duality
Our work: extends special case of a result of Aminian et al. (2024) to non-discrete reward distributions
Pandora's Box Gittins Index for Bayesian Optimization
Bayesian optimization: posterior distribution is correlated
Define Pandora's Box Gittins Index acquisition function:
$\alpha^{\f{PBGI}}(x) = g$ where $g$ solves $\f{EI}_{f\given y}(x; g) = c(x)$
Correlations: incorporated into acquisition function via the posterior
Effect of cost-per-sample hyperparameter
$\lambda$: controls risk-averse vs. risk-seeking behavior
Limit as $\lambda\to0$: converges to UCB with automatic learning rate
Can we outperform expected improvement per unit cost?
Counterexample: random objective with high-variance high-cost region
Pandora's Box Gittins Index: still performs well
Experiments
Experiments
: Bayesian Regret
Objective functions: sampled from the prior
Synthetic Benchmark Functions
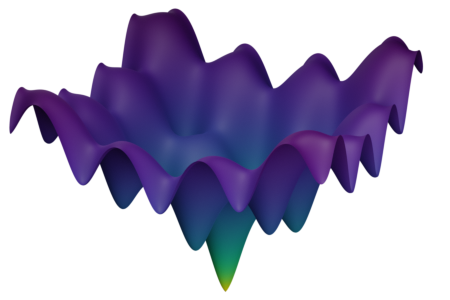
Ackley function
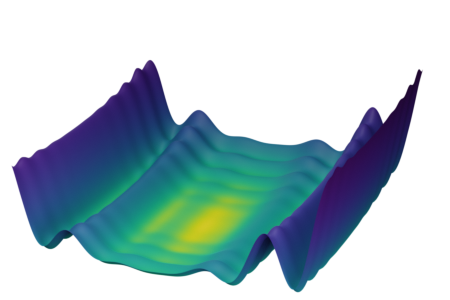
Levy function
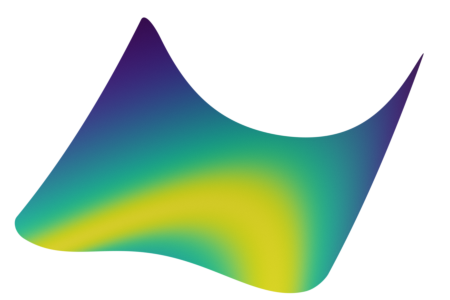
Rosenbrock function
Synthetic Benchmark Functions
Empirical Objectives
Conclusions
Novel acquisition function: Pandora's Box Gittins Index
- Settings: expected budget-constrained and cost-per-sample
- Works in heterogeneous-cost setting and for uniform costs
- Closely-related to both expected improvement and UCB
- Exact optimality in simplified problem: orthogonal insights
Performance of Pandora's Box Gittins Index
- Sufficiently-easy low-dim. problems: comparable to baselines
- Too-difficult high-dim. problems: similar to random search
- Medium-hard problems of moderate dim.: strong performance
- Can compete with state-of-the-art non-myopic approaches
Gittins Index Theory
What can
Gittins Index Theory
do?
Gittins Index Theory
- Workhorse tool in queuing theory
- Minimize expected wait time: serve short jobs first
Bayesian Optimization: high-dimension and complex feedback models
- Freeze-thaw
- Continuous-time and asynchronous
- Bayesian quadrature
- Function networks
- Exact optimality in simplified problems without dependence
Unexplored toolkit with which to understand decision-making
Thank you!
https://avt.im/· @avt_im
Thank you!
https://avt.im/· @avt_im

UAI Tutorial on Geometric Probablistic Models
Available on my website - check it out!
Thank you!
https://avt.im/· @avt_im
Q. Xie, R. Astudillo, P. Frazier, Z. Scully, and A. Terenin. Cost-aware Bayesian optimization via the Pandora's Box Gittins index. arXiv:2406.20062, 2024.